Vehicle Tracking Environment¶

The VehicleTrackingEnv is a custom Gymnasium environment specifically focusing on a pursuit-evasion or following scenario on a 2D grid. A single decision-making agent controls one or more Pursuers.

Environment Description¶

The VehicleTrackingEnv simulates a grid-based scenario where one or more Pursuers ($\mathbf{P}$) attempt to either capture an Evader ($\mathbf{E}$) or simply follow it, depending on the game_mode. The environment takes place on a grid map that can contain obstacles ($\mathbf{X}$).

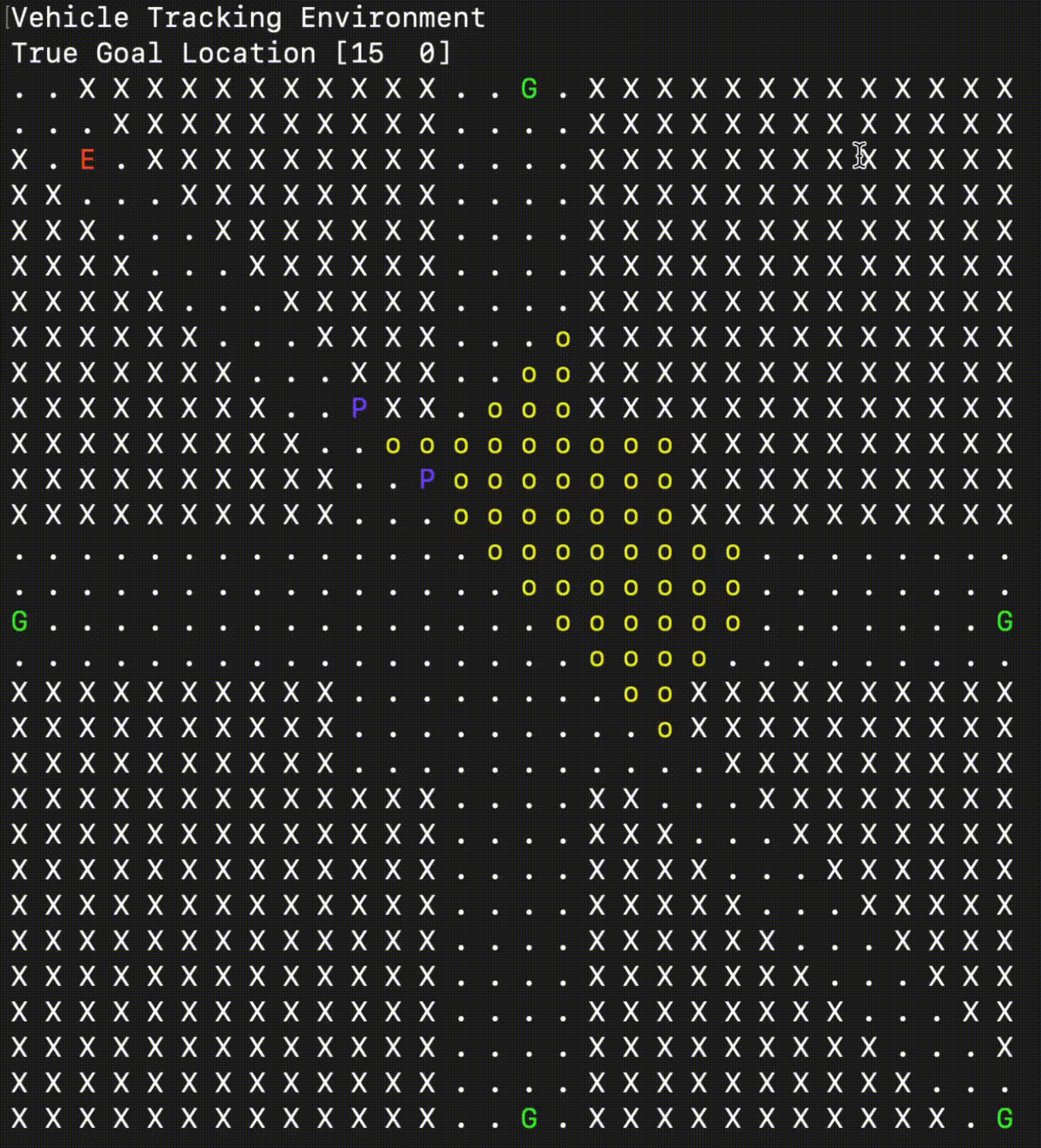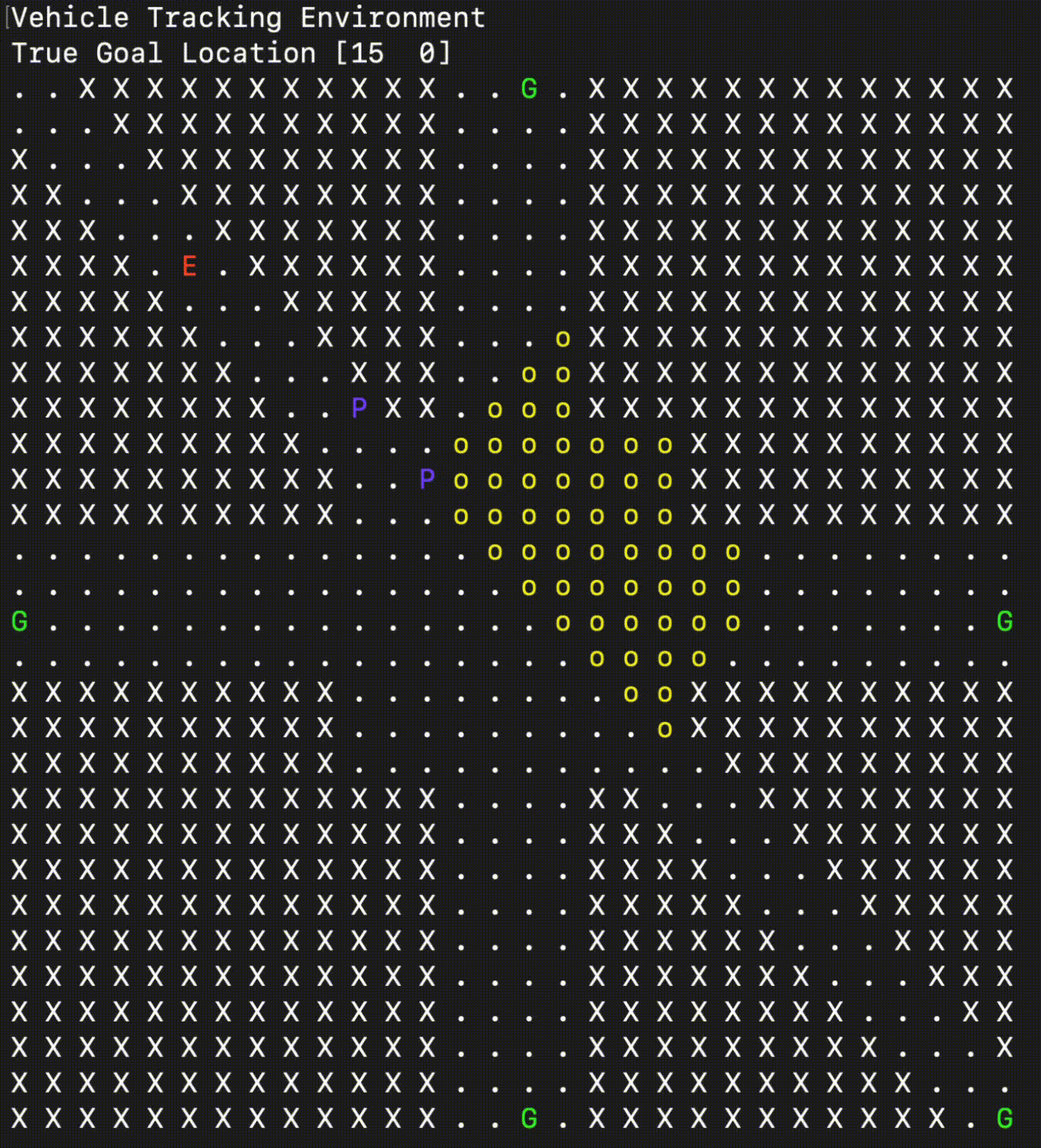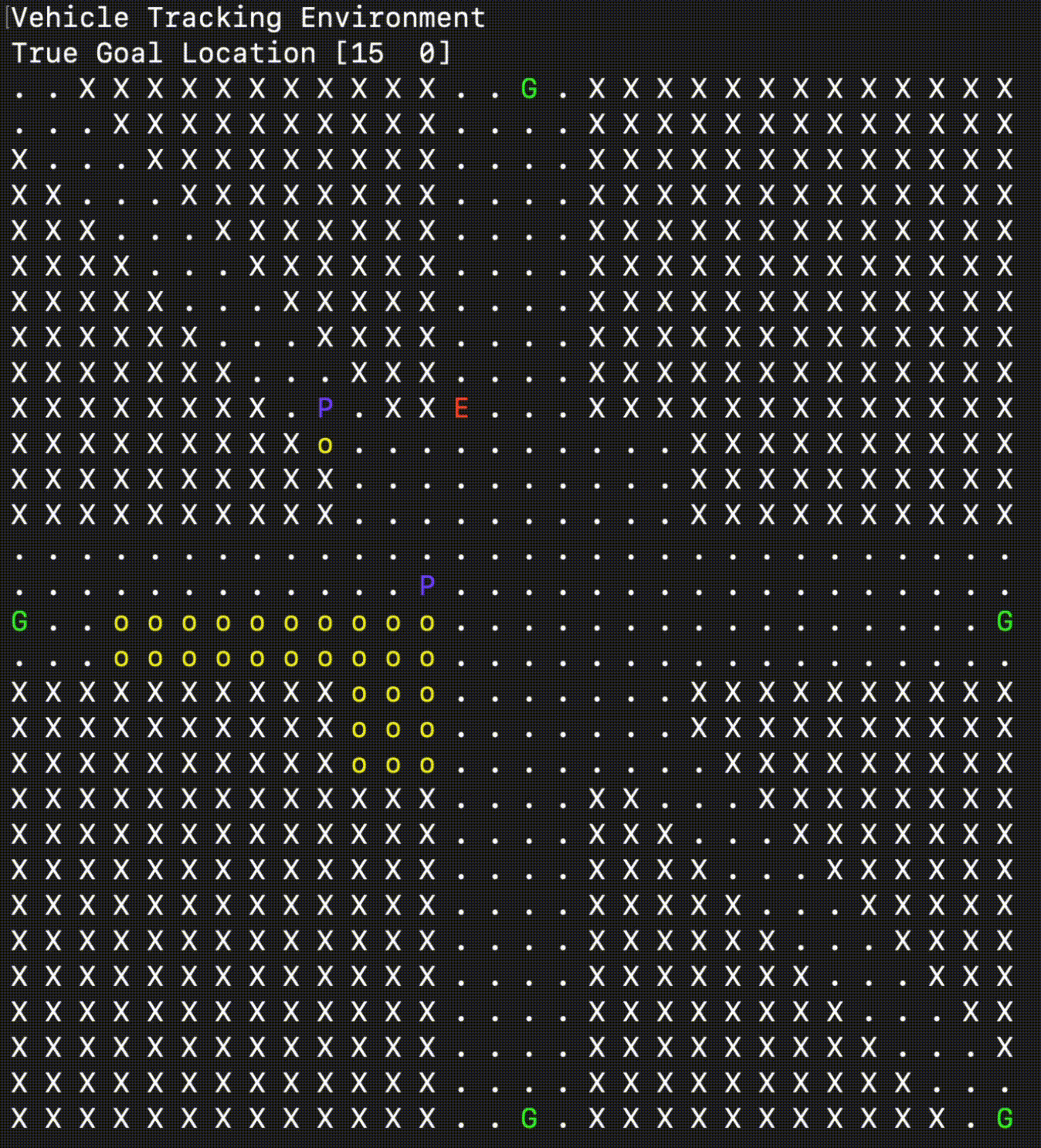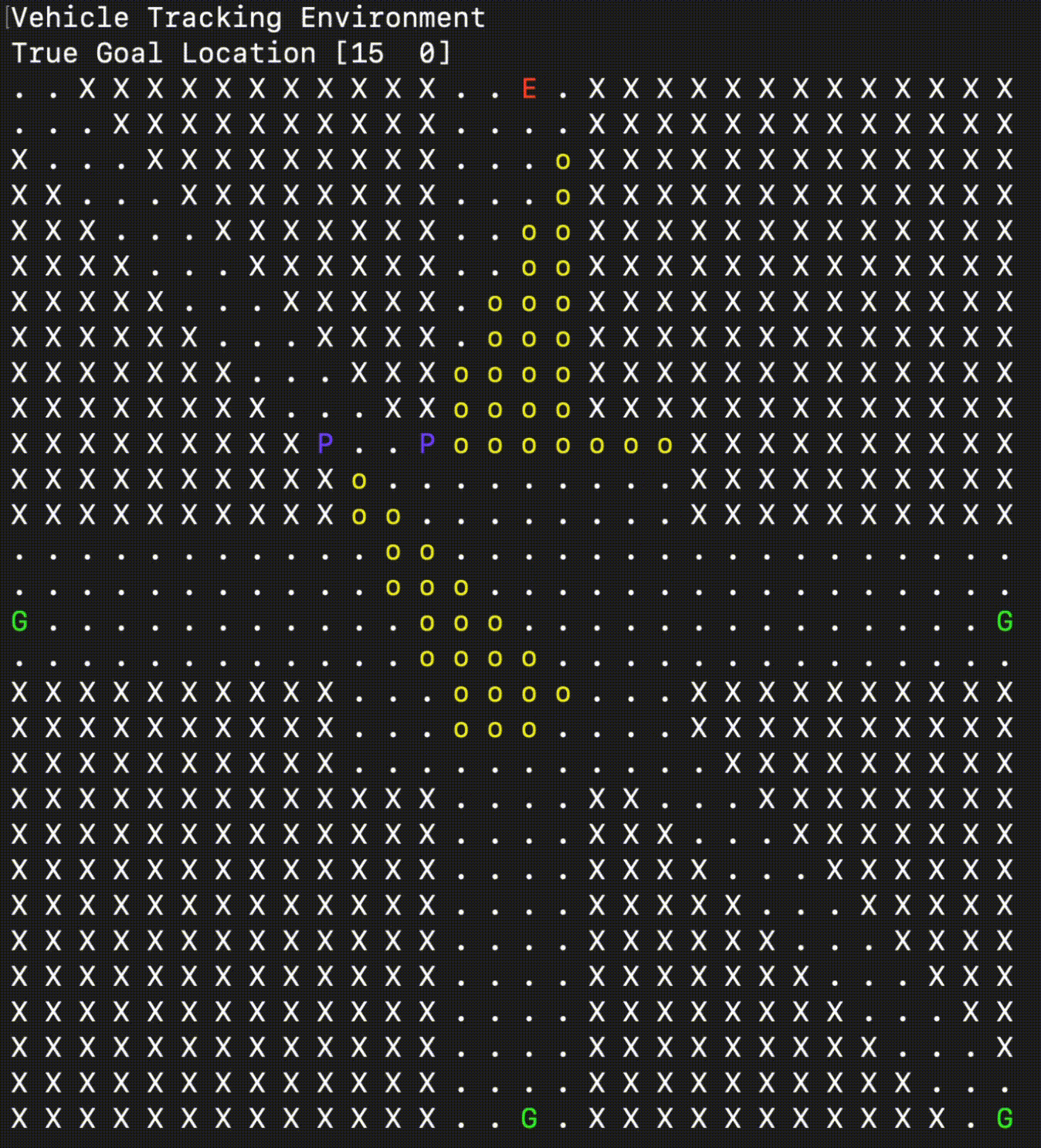
Vehicle Tracking Animation The Vehicle Tracking Environment.

The Evader follows a pre-computed, shortest path towards a randomly selected Goal ($\mathbf{G}$) location. The Pursuers are the agents controlled by the policy and must navigate the map while respecting obstacles and, optionally, their limited Field of View (FOV).

Element	Symbol (Render)	Color
Pursuer	$\mathbf{P}$	Blue (`\033[94mP\033[0m`)
Evader	$\mathbf{E}$	Red (`\033[91mE\033[0m`)
Goal	$\mathbf{G}$	Green (`\033[92mG\033[0m`)
Obstacle	$\mathbf{X}$	Default
Visible Cell	$\mathbf{o}$	Yellow (`\033[93mo\033[0m`)
Empty Cell	$\mathbf{.}$	Default

The coordinate system is (column, row), with the origin $(\mathbf{0, 0})$ at the top-left corner.

Action Space¶

The action space is a MultiDiscrete space, where the size of the array is equal to the number of pursuers (num_pursuers). Each element is an integer representing one of the 11 possible actions for an individual pursuer.

\[ \text{Action Space} = \text{spaces.MultiDiscrete}([11] \times \text{num_pursuers}) \]

Action Name	Action Value	Description
$\mathbf{STAY}$	$\mathbf{0}$	Remain in the current cell.
$\mathbf{UP}$	$\mathbf{1}$	Move one cell North (decreases row index).
$\mathbf{DOWN}$	$\mathbf{2}$	Move one cell South (increases row index).
$\mathbf{LEFT}$	$\mathbf{3}$	Move one cell West (decreases column index).
$\mathbf{RIGHT}$	$\mathbf{4}$	Move one cell East (increases column index).
$\mathbf{UP\_LEFT}$	$\mathbf{5}$	Move one cell North-West.
$\mathbf{UP\_RIGHT}$	$\mathbf{6}$	Move one cell North-East.
$\mathbf{DOWN\_LEFT}$	$\mathbf{7}$	Move one cell South-West.
$\mathbf{DOWN\_RIGHT}$	$\mathbf{8}$	Move one cell South-East.
$\mathbf{ROTATE\_CW}$	$\mathbf{9}$	Rotate the pursuer’s $\mathbf{FOV}$ $\mathbf{Clockwise}$.
$\mathbf{ROTATE\_CCW}$	$\mathbf{10}$	Rotate the pursuer’s $\mathbf{FOV}$ $\mathbf{Counter-Clockwise}$.

Movement actions are constrained by map boundaries and obstacles. Rotation actions update the pursuer’s direction index, which is used for the Field of View calculations.

Observation Space¶

The observation space is a dictionary containing the flattened grid indices of all active entities.

\[ \text{Observation Space} = \text{spaces.Dict}(\{ \dots \}) \]

Key	Type	Description
$\mathbf{pursuer\_position}$	$\text{spaces.MultiDiscrete}$	Array of flattened grid indices for $\mathbf{P}$ positions. Shape is $(\text{num\_pursuers},)$.
$\mathbf{evader\_position}$	$\text{spaces.Box}$	Flattened grid index for the $\mathbf{E}$’s position. Returns -1 if the $\mathbf{E}$ is not in view of any $\mathbf{P}$ and $\mathbf{is\_evader\_always\_observable}$ is $\mathbf{False}$ (Partial Observability).
$\mathbf{goal\_position}$	$\text{spaces.MultiDiscrete}$	Array of flattened grid indices for all possible $\mathbf{G}$ locations. The true goal is not explicitly revealed.

Positions are converted from $\mathbf{(col, row)}$ to a flattened index $i$ using: $$i = \text{column} \times \text{Map_Height} + \text{row}$$

Reward Structure and Termination¶

Capture Reward (if game_mode="capture"): $\mathbf{+1.0}$ if any $\mathbf{P}$ is on the $\mathbf{E}$’s cell.
Follow Reward (if game_mode="follow"): $\mathbf{+1.0}$ if the $\mathbf{E}$ is in view of any $\mathbf{P}$.
Capture Distance Reward (if game_mode="capture" and $\mathbf{E}$ is in view): $\mathbf{1.0} / (\text{min\_distance} + \mathbf{1})$, where $\text{min\_distance}$ is the shortest Euclidean distance from any $\mathbf{P}$ to the $\mathbf{E}$.
Zero Reward: $\mathbf{0.0}$ in all other cases.

The episode terminates ($\mathbf{done=True}$) if:

The $\mathbf{E}$ reaches its hidden $\mathbf{Goal}$ location.
The $\mathbf{E}$ is $\mathbf{captured}$ by a $\mathbf{P}$ (only if game_mode="capture").

Non-Stationarity Focus: Structural Changes¶

The environment is particularly well-suited for simulating $\mathbf{Structural}$ $\mathbf{Non-Stationarity}$ through agent failure or $\mathbf{coalition}$ $\mathbf{breakdown}$. The Corresponding NS-Gym wrapper can modify the num_pursuers parameter at specified timesteps to simulate scenarios where agents become non-operational or leave the coalition, requiring the remaining agents to adapt their strategies dynamically.

Tunable Parameters (NS-Gym)¶

This environment is designed with several parameters that can be varied, which can be leveraged by an NS-Gym wrapper to induce non-stationarity. You got it. Here is the revised table with the obstacle_map parameter removed, the NS-Gym Use Case merged into the Description, and the separate NS-Gym Use Case column deleted.

Parameter	Type	Default	Description
$\mathbf{num\_pursuers}$	$\text{int}$	$\mathbf{1}$	Number of pursuer agents. This can be used to induce $\mathbf{Structural}$ $\mathbf{Change}$ by varying the number of active agents (e.g., simulating agent failure by setting some to $\mathbf{STAY}$ or removing them from dynamics).
$\mathbf{fov\_distance}$	$\text{float}$	$\mathbf{2}$	Maximum vision range of each pursuer. Used to introduce $\mathbf{Environmental}$ $\mathbf{Drift}$ by gradually or abruptly changing the vision capability.
$\mathbf{fov\_angle}$	$\text{float}$	$\mathbf{\pi / 2}$	Angular width of the pursuer’s Field of View. Used to introduce $\mathbf{Environmental}$ $\mathbf{Drift}$ by changing the angular vision capability.
$\mathbf{game\_mode}$	$\text{str}$	$\mathbf{"capture"}$	Determines the reward/termination logic: $\mathbf{"capture"}$ or $\mathbf{"follow"}$. Used for $\mathbf{Reward}$ $\mathbf{Non-Stationarity}$ by switching the optimization goal and reward function.
$\mathbf{is\_evader\_always\_observable}$	$\text{bool}$	$\mathbf{True}$	If $\mathbf{False}$, the $\mathbf{E}$’s position is -1 outside any $\mathbf{P}$’s FOV. Used for $\mathbf{Observation}$ $\mathbf{Non-Stationarity}$ by switching between fully observable ($\mathbf{True}$) and partially observable ($\mathbf{False}$) modes.
$\mathbf{allow\_diagonal\_evader\_movement}$	$\text{bool}$	$\mathbf{False}$	Whether the $\mathbf{E}$’s path can include diagonal moves. Used to modify $\mathbf{Evader}$ $\mathbf{Dynamics}$ by changing the mobility of the target.
$\mathbf{goal\_locations}$	$\text{np.ndarray}$	$\mathbf{[(H/2, W/2)]}$	Set of possible destinations for the $\mathbf{E}$. Used to modify $\mathbf{Evader}$ $\mathbf{Behavior}$ by changing the target space of the $\mathbf{E}$.

Action Name	Action Value	Description
\(\mathbf{STAY}\)	\(\mathbf{0}\)	Remain in the current cell.
\(\mathbf{UP}\)	\(\mathbf{1}\)	Move one cell North (decreases row index).
\(\mathbf{DOWN}\)	\(\mathbf{2}\)	Move one cell South (increases row index).
\(\mathbf{LEFT}\)	\(\mathbf{3}\)	Move one cell West (decreases column index).
\(\mathbf{RIGHT}\)	\(\mathbf{4}\)	Move one cell East (increases column index).
\(\mathbf{UP\_LEFT}\)	\(\mathbf{5}\)	Move one cell North-West.
\(\mathbf{UP\_RIGHT}\)	\(\mathbf{6}\)	Move one cell North-East.
\(\mathbf{DOWN\_LEFT}\)	\(\mathbf{7}\)	Move one cell South-West.
\(\mathbf{DOWN\_RIGHT}\)	\(\mathbf{8}\)	Move one cell South-East.
\(\mathbf{ROTATE\_CW}\)	\(\mathbf{9}\)	Rotate the pursuer’s \(\mathbf{FOV}\) \(\mathbf{Clockwise}\).
\(\mathbf{ROTATE\_CCW}\)	\(\mathbf{10}\)	Rotate the pursuer’s \(\mathbf{FOV}\) \(\mathbf{Counter-Clockwise}\).

Key	Type	Description
\(\mathbf{pursuer\_position}\)	\(\text{spaces.MultiDiscrete}\)	Array of flattened grid indices for \(\mathbf{P}\) positions. Shape is \((\text{num\_pursuers},)\).
\(\mathbf{evader\_position}\)	\(\text{spaces.Box}\)	Flattened grid index for the \(\mathbf{E}\)’s position. Returns -1 if the \(\mathbf{E}\) is not in view of any \(\mathbf{P}\) and \(\mathbf{is\_evader\_always\_observable}\) is \(\mathbf{False}\) (Partial Observability).
\(\mathbf{goal\_position}\)	\(\text{spaces.MultiDiscrete}\)	Array of flattened grid indices for all possible \(\mathbf{G}\) locations. The true goal is not explicitly revealed.

Parameter	Type	Default	Description
\(\mathbf{num\_pursuers}\)	\(\text{int}\)	\(\mathbf{1}\)	Number of pursuer agents. This can be used to induce \(\mathbf{Structural}\) \(\mathbf{Change}\) by varying the number of active agents (e.g., simulating agent failure by setting some to \(\mathbf{STAY}\) or removing them from dynamics).
\(\mathbf{fov\_distance}\)	\(\text{float}\)	\(\mathbf{2}\)	Maximum vision range of each pursuer. Used to introduce \(\mathbf{Environmental}\) \(\mathbf{Drift}\) by gradually or abruptly changing the vision capability.
\(\mathbf{fov\_angle}\)	\(\text{float}\)	\(\mathbf{\pi / 2}\)	Angular width of the pursuer’s Field of View. Used to introduce \(\mathbf{Environmental}\) \(\mathbf{Drift}\) by changing the angular vision capability.
\(\mathbf{game\_mode}\)	\(\text{str}\)	\(\mathbf{"capture"}\)	Determines the reward/termination logic: \(\mathbf{"capture"}\) or \(\mathbf{"follow"}\). Used for \(\mathbf{Reward}\) \(\mathbf{Non-Stationarity}\) by switching the optimization goal and reward function.
\(\mathbf{is\_evader\_always\_observable}\)	\(\text{bool}\)	\(\mathbf{True}\)	If \(\mathbf{False}\), the \(\mathbf{E}\)’s position is -1 outside any \(\mathbf{P}\)’s FOV. Used for \(\mathbf{Observation}\) \(\mathbf{Non-Stationarity}\) by switching between fully observable (\(\mathbf{True}\)) and partially observable (\(\mathbf{False}\)) modes.
\(\mathbf{allow\_diagonal\_evader\_movement}\)	\(\text{bool}\)	\(\mathbf{False}\)	Whether the \(\mathbf{E}\)’s path can include diagonal moves. Used to modify \(\mathbf{Evader}\) \(\mathbf{Dynamics}\) by changing the mobility of the target.
\(\mathbf{goal\_locations}\)	\(\text{np.ndarray}\)	\(\mathbf{[(H/2, W/2)]}\)	Set of possible destinations for the \(\mathbf{E}\). Used to modify \(\mathbf{Evader}\) \(\mathbf{Behavior}\) by changing the target space of the \(\mathbf{E}\).

Element	Symbol (Render)	Color
Pursuer	\(\mathbf{P}\)	Blue (`\033[94mP\033[0m`)
Evader	\(\mathbf{E}\)	Red (`\033[91mE\033[0m`)
Goal	\(\mathbf{G}\)	Green (`\033[92mG\033[0m`)
Obstacle	\(\mathbf{X}\)	Default
Visible Cell	\(\mathbf{o}\)	Yellow (`\033[93mo\033[0m`)
Empty Cell	\(\mathbf{.}\)	Default